Menschen mit Schizophrenie reagieren anders als Gesunde auf optischen Täuschungen. Ist das ein Hinweis auf veränderte Abläufe im Gehirn? Dieser Frage gehen Wissenschaftlerinnen und Wissenschaftler mit Hilfe eines mathematischen Modells nach.
Wahnvorstellungen und Realitätsverlust sind wesentliche Symptome einer Schizophrenie. Es wird vermutet, dass diese unter anderem durch eine fehlerhafte Vorhersagefähigkeit des Gehirns entstehen: Die Patientinnen und Patienten können neue Sinneswahrnehmungen nicht korrekt mit ihren Erinnerungen und den erlernten Vorhersagen ihres Gedächtnisses zur Deckung bringen. Eine Möglichkeit, diese Einschränkung in der Wahrnehmung von Menschen mit Schizophrenie genauer zu untersuchen, ist ihre Reaktion auf optische Täuschungen. Denn sie nehmen diese oftmals anders wahr als Gesunde.
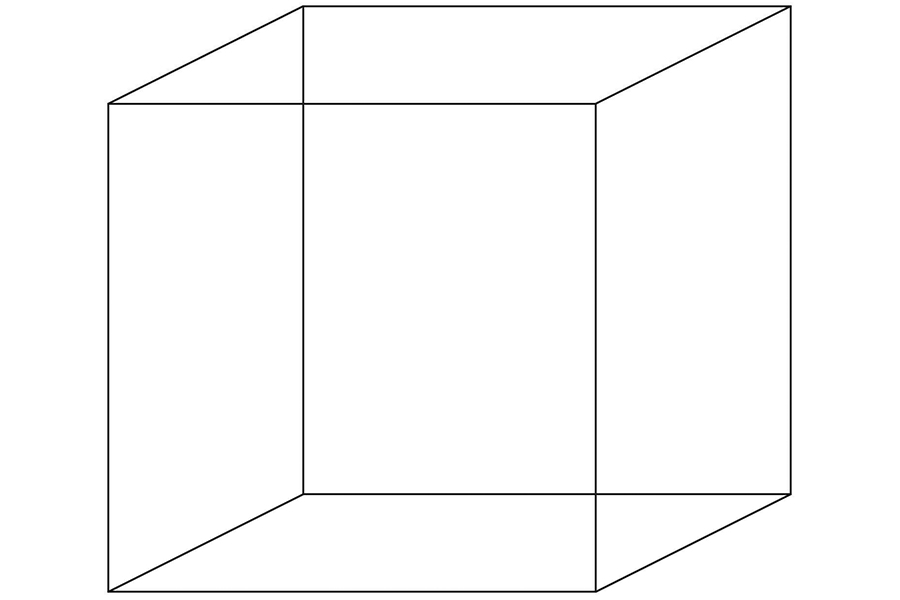
Der Necker-Würfel: Diese nach dem Schweizer Physiker Albert Necker (1786–1793) benannte Kippfigur ist ein bekanntes Beispiel für eine optische Täuschung.
DLR-PT erstellt nach L. Albert Necker
Ein bekanntes Beispiel für eine optische Täuschung ist ein dreidimensional dargestellter Würfel, der Necker-Würfel. Bei längerer Betrachtung wechselt unsere Wahrnehmung immer wieder zwischen zwei Ansichten: Wir sehen den Würfen entweder „von unten“ oder „von oben“. Man nennt eine solche optische Täuschung einen bi-stabilen Stimulus und dieser ruft eine bi-stabile Wahrnehmung hervor. „Interessanterweise haben Studien unserer Verbundpartner an der Berliner Charité um Dr. Katharina Schmack ergeben, dass der Prozess der bi-stabilen Wahrnehmung bei Personen mit Schizophrenie andere Charakteristika aufweist als bei Gesunden. Und dies kann ein Hinweis auf eine veränderte neuronale Aktivität im Gehirn der Betroffenen sein“, erklärt die Mathematikerin Professor Gaby Schneider von der Goethe Universität Frankfurt. Sie ist eine Projektleiterin im interdisziplinären Juniorverbund „PsychoSys“, der vom Bundesministerium für Bildung und Forschung (BMBF) gefördert wird.
Wer wechselt die Perspektive und wie oft?
So zeigen Patientinnen und Patienten mit Schizophrenie bei der Präsentation eines bi-stabilen Stimulus etwas seltener einen spontanen Wechsel zwischen den Wahrnehmungsperspektiven. Präsentieren die Forscherinnen und Forscher den bi-stabilen Stimulus hingegen mit kurzen Unterbrechungsintervallen, ist die Zahl der Perspektivwechsel bei Schizophrenen etwas höher im Vergleich zu gesunden Testpersonen. Beobachtet wurde, so die Wissenschaftlerin, dass die Patientinnen und Patienten mit Schizophrenie ebenso wie Gesunde eine einzelne Perspektive auch über einen längeren Zeitraum stabil wahrnehmen können. Es gibt aber auch Zeitabschnitte, in denen sie immer wieder in rascher Abfolge zwischen den Perspektiven wechseln. „Generell befinden sich Personen mit Schizophrenie deutlich häufiger in einem solchen instabilen Zustand der Wahrnehmung als Gesunde. Dies passt zu der Beobachtung, dass Patientinnen und Patienten mit Schizophrenie eine erhöhte Anfälligkeit besitzen, sich von irrelevanten Informationen ablenken zu lassen“, beschreibt Schneider.
Mathematik und Praxis in Einklang bringen
Ein Ziel des Juniorverbundes PsychoSys war es, zunächst ein mathematisches Modell zu entwerfen, das diese Veränderungen in der Wahrnehmung von Patientinnen und Patienten mit Schizophrenie exakt beschreiben kann. Ein solches Modell erlaubt anschließend Vorhersagen über die zugrunde liegenden neuronalen Prozesse. Durch die enge Kooperation von Forscherinnen und Forschern aus der Mathematik, Medizin und Psychologie ist es Schneider und ihrem Doktoranden Stefan Albert gelungen, ein theoretisch fundiertes mathematisches Modell zu entwickeln, das gleichzeitig so einfach ist, dass es auch in der Praxis angewendet werden kann. „Das mag banal klingen, aber genau das war die Schwierigkeit. Denn zuweilen können die theoretischen Modelle in ihrer mathematischen Schönheit und Eleganz nicht mit den bei Patientinnen und Patienten gemessenen Daten in Einklang gebracht werden. Oder aber es werden mathematische Modelle erstellt, die zwar Erklärungen für Prozesse im Gehirn liefern und vielerlei Daten beschreiben können, die aber so viele Stellschrauben besitzen, dass ein Effekt nicht mehr eindeutig zugeordnet werden kann“, erklärt Schneider.
Mit Hilfe des Modells können die Wissenschaftler nun empirische Daten zur Wahrnehmung von optischen Täuschungen in Beziehung setzen zu möglichen neuronalen Prozessen im Gehirn. „Durch die Unterschiede zwischen Gesunden und Patientinnen und Patienten mit Schizophrenie können wir Hypothesen über die zugrundeliegenden neuronalen Prozesse gewinnen“, sagt Schneider.
Juniorverbünde in der Systemmedizin
Mit der Förderung von Juniorverbünden in der Systemmedizin sollen jüngere Wissenschaftlerinnen und Wissenschaftler verschiedener Fachdisziplinen die Möglichkeit erhalten, hochinnovative Forschungsvorhaben der Systemmedizin in einem interdisziplinären Team umzusetzen. Dies soll es ihnen erleichtern, sich über die Grenzen ihrer Fachdisziplinen hinweg zu vernetzen, wissenschaftliche Expertise aufzubauen und sich in der systemorientierten medizinischen Forschung zu etablieren. Seit 2014 fördert das BMBF neun interdisziplinäre Juniorverbünde mit ca. 16 Mio. Euro.
Wettstreit der Neuronen ist Basis für das Modell
Für die Konstruktion ihres mathematischen Modells für optische Täuschungen haben die Wissenschaftlerinnen und Wissenschaftler ausgenutzt, dass neuronale Prozesse bei bi-stabiler Wahrnehmung oft mit dem folgenden Modell beschrieben werden können: Zwei Gruppen von Nervenzellen stehen dabei im „Wettstreit“. Gewinnt Gruppe A, sind also die Neuronen dieser Gruppe aktiver als die der anderen Gruppe, nehmen wir Perspektive A wahr. Gewinnt hingegen Gruppe B, nehmen wir Perspektive B wahr. Im zweiten Schritt des Modells wird ein weiterer, ähnlicher Wettstreit auf einer höheren neuronalen Ebene angenommen, der den Wechsel zwischen stabiler und instabiler Wahrnehmung hervorruft. „Unser Modell beschreibt im einfachsten Fall mit nur zwei Parametern diesen Wettstreit der Neuronen. So können wir den resultierenden Wechsel der Perspektive und – mit weiteren Parametern – auch den Zustand stabiler beziehungsweise instabiler Wahrnehmung beschreiben. Vergleichbare Modelle benötigen hierfür in der Regel deutlich mehr Parameter, was die Anpassung an empirische Datensätze erschwert“, beschreibt Schneider.
Das mathematische Modell bietet einen wichtigen Ansatzpunkt, um die kognitiven Einschränkungen bei Schizophrenie zukünftig besser zu verstehen. Zudem könnte es zur Entwicklung diagnostischer Tests beitragen, die bei der Frage unterstützen, ob ein Mensch an Schizophrenie leidet oder nicht.
Den Nachwuchs für Systemmedizin begeistern
Um auch den wissenschaftlichen Nachwuchs für das interdisziplinäre Forschungsgebiet der Systemmedizin zu begeistern und an die Anwendung der Mathematik in der Praxis heranzuführen, bietet der Juniorverbund PsychoSys in Frankfurt eine spezielle Lehrveranstaltung an. „Unser statistisches Praktikum ist für alle – für die Studierenden der Mathematik, aber auch für die Lehrenden und Forschenden – eine äußert gewinnbringende Veranstaltung. Sie erlaubt es, diverse Analyseansätze für aktuelle Datensätze und Fragestellungen zu entwickeln und gemeinsam zu erproben. Gleichzeitig stellen wir den Kontakt zwischen Studierenden und Anwendern her“, sagt Schneider.
Was ist Systemmedizin?
Die „Systembiologie“ will die dynamischen Lebensprozesse der Zellen, Gewebe, Organe und Organismen verstehen sowie die zugrundeliegenden Wechselwirkungen auf molekularer Ebene in Netzwerken abbilden. Dazu wendet sie Methoden der mathematischen Modellierung und die Leistungskraft moderner Computer an. Die „Systemmedizin“ will die Erkenntnisse und Methoden der Systembiologie auf die Medizin übertragen und für Patientinnen und Patienten nutzbar machen. Das Ziel der Systemmedizin ist es, die neuen Einsichten in die Prozesse des Lebens anzuwenden, um Krankheiten genauer zu diagnostizieren und besser zu behandeln. Denn ob ein Mensch gesund oder krank ist, hängt von vielen Faktoren ab, seien es genetische Unterschiede, die Veränderung von Molekülen oder Umwelteinflüsse. Die Frage ist, wie all diese Faktoren und Systeme ineinandergreifen und wie sie zu beeinflussen sind.
Ansprechpartnerin:
Prof. Dr. Gaby Schneider
Institut für Mathematik
Goethe-Universität
Robert-Mayer-Straße 10
60325 Frankfurt am Main
schneider@math.uni-frankfurt.de
